학위논문통계

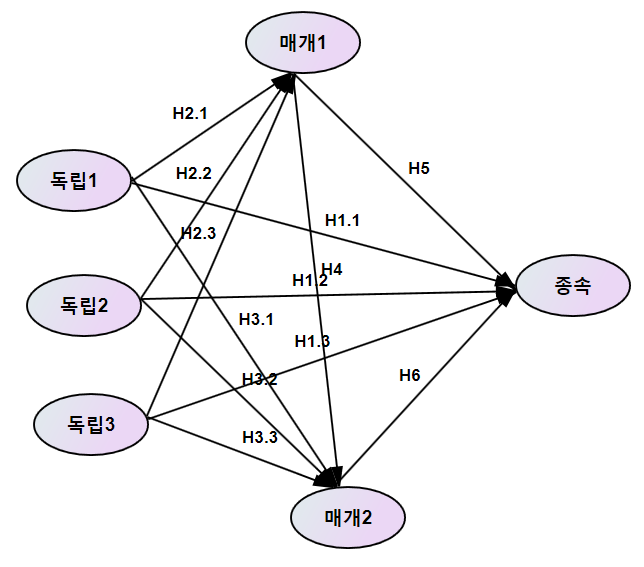
독립변수가 하나가 아니라 여러개가 있는 경우 다중회귀분석이라고 하여 단순회귀분석과 구별을 하는데 사실 통계학에서는 구별을 하지 않습니다. 이런 구별은 대학교 1학년 기초 통계학에서 구별을 하죠. 오늘은 독립변수가 여러개, 즉 X1, X2, X3가 있다고 하죠. 그럼 회귀모형식은  Y=b0+b1*X1+b2*X2+b3*X3+e  이라 하죠.   1. 독립변수가 서로간 독립인 경우  : 상관계수를 구해 보니까 독립변수들간에 상관계수가 전부 0일 경우 이 경우 특별히 2개의 독립변수가 orthogonal 하다는 표현을 씁니다. 현실에서는 절대로 나올 수 없지만 이론적으로 만들 수가 있습니다.  탐색적 요인분석을 하여 요인점수를 저장하여 이 요인점수를 독립변수로 사용하면 됩니다. 이 경우 요인점수는 표준화되어 있..

1. white noise 시계열 꼭 정규분포일 필요는 없지만 독립적이고 같은 분포를 갖는 시계열를 말합니다.  R 코드는 whiteplot(1:1000, white, type="l", col=6);  2. random walk  주식시장을 보면 이동평균선이라는 그래프를 제공해주죠. 사실 이동평균선이 아니라 자기회귀가 이론적으로 더 맞는 말입니다.   AR(1) process를 보면 Y(t)=a*Y(t-1)+e(t) 이렇게 정의됩니다.  여기서 a=1이면 random walk이라고 한다. 이 경우 비정상시계열 모양을 합니다. a=1이면 Y(t)=Y(t-1)+e(t) 현재 시점 t에서 변수의 값 Y(t)는 하나 전 시점 (t-1)의 변수의 값 Y(t-1)과 같기 때문에 Y(t)는 정상시계열이라고 착각하기 ..

회귀분석에 나오는 기본적인 개념도 잘 모르시는 분들이 계셔서 오늘은 상관계수와 단순회귀분석의 예를 들어서 회귀분석 결과물을 설명하겠습니다.   2개의 변수 X와 Y의 상관계수를 구하면 0.815가 나옵니다. 이 경우 Y를 종속변수, X를 독립변수로 하여 단순회귀분석을 하면 다음과 같은 결과를 얻을 수 있습니다.   독립변수비표준표준t pBs.e.베타상수0.9120.151.6.0560.000X0.7890.0360.81522.1100.000***모형통계량R=0.815, R2=0.663, F=488.847, p=0.000***  비표준의 경우 원 변수 X, Y를 써서 회귀분석을 한 경우이고 표준의 경우 변수 X, Y를 표준화, 즉 평균이 0이고 표준편차가 1인 변수로 변환을 한 다음 회귀분석을 한 결과이다. ..

시계열 회귀분석에는 두 가지 방법이 있다고 했습니다.  하나는 정상시계열로 변환하여 회귀분석하는 방법이 있고, 또 하나는 비정상시계열이라도 공적분(cointegration) 관계가 있으면 비정상시계열 변수 그대로 사용할 수 있습니다. 현실에서는 우선 공적분 관계가 있는지 확인하고 공적분관계가 있으면 바로 원 변수를 가지고 회귀분석을 합니다. 이때 stata에서는 vecm 명령어를 사용해야 합니다. 공적분을 이해하기 위해서는 우선 적분과정(integration process)라는 말을 이해를 해야 합니다. 그런데 개념은 별개 아닙니다.  원 변수가 정상시계열이면 I(0)이라고 표시하고 원 변수가 비정상시계열인데 1차 차분한 자료가 정상시계열로 바뀌면 I(1)으로 표시합니다. 2번 차분해야 정상시계열로 바뀌..

계량경제 이론을 이용한 통계 분석 방법론으로는 크게 2가지로 나눌 수 있습니다. 하나는 시계열 회귀분석 방법이고 또 하나는 패널 회귀분석 방법입니다. 시계열 회귀분석은 제가 편의상 사용하는 용어입니다.  여기서 몇 가지 언급을 하자면 1. 일단 두 분석 방법은 데이터의 형태가 완전히 다릅니다. 이걸 먼저 구별할 줄 알아야 하고요. 2. 그리고 또 하나는 시계열 회귀분석은 통상 VECM이라는 모형으로 하는 경우가 많고 패널회귀분석은 고정효과모형과 확률효과모형을 구별하는 정도만 하시면 됩니다.  3. 계량 경제 논문을 제대로 쓰고 싶어서 공부를 하려고 하면 대부분 조금 하다가 좌절을 하게 됩니다. 먼저 일반적인 회귀분석 이론부터 출발해서 백색잡음(white noise), 임의 행보(random walk), ..

오늘은 박사수준의 구조방정식 모형을 소개하고자 합니다. 박사수준의 구조방정식 모형은 통상 석사수준의 구조방정식 모형에다 조절효과를 보는 것입니다. 여기서 조절효과를 본다는 것은 구조방정식 책에 있는 다중집단 분석을 한다는 이야기입니다. 우선 간단한 모형을 소개해보죠. A ==> B ==> C, 즉 독립변수 A, 매개변수 B, 종속변수 C가 있는 구조방정식 인과모형이 있다고 하죠. 여기에 조절변수 D를 끼워 넣는다는 것입니다. 예를 들어 설명하면 지난번 석사수준의 구조방정식 소개 글처럼 A은 운동량, C는 몸무게, B는 식욕이라고 하죠. 그림으로 그리면 운동량, 식욕, 체중과의 인과관계의 결과가 남자와 여자인 경우 다를 수가 있고, 또 비만이 사람과 아닌 사람에 따라 결과가 달라질 수 있습니다. 남자와 여..

1. 연구모형이 왜 중요한가 연구모형 자체가 논문의 주제이고 연구가설이고 그리고 이를 한글로 풀어내면 논문의 제목이 됩니다. 예를 들어 연무고형에 독립변수, 매개변수, 종속변수가 있다고 하면 논문 제목은 “독립변수가 종속변수에 미치는 영향에 대한 연구: 매개변수의 매개효과를 중심으로” 또는 “독립변수가 매개변수를 매개로 종속변수에 미치는 구조적 관계에 대한 연구” 이렇게 논문제목을 답니다. 따라서 연구모형에 나오는 개념을 잘 이해하는 것이 매우 중요합니다.  2. 구조방정식 모형:  통상 연구모형에 매개변수가 들어가 있는 모형을 구조방정식 모형이라 합니다. 정확하게는 연구변수들간의 연립방정식 모형을 구조방정식이라 하지만 이런 내용은 너무 전문적이라 생략하고요. 이 구조방정식 모형을 분석하려면 통상 AMO..

가장 흔하게 사용되는 연구모형을 한번 알아 보겠습니다. 석사 논문에서는  1) 조절효과를 보는 것 2) 구조방정식 모형에서는 독립변수 3-4개 , 매개변수 1개, 종속변수 1개 정도로 좀 간단한 구조방정식 모형을 봅니다.   박사논문에서는  거의 다 구조방정식 모형으로 하는데 이 경우 매개변수 2-3개 정도로 합니다. 그리고 조절효과를 보는 다중집단 분석을 같이 하고요.  물론 이런 인과관계를 보는 논문 말고 학과의 성격에 따라 실험의 효과를 보는 논문이 있습니다.   그럼 위에 언급한 모형을 조금 자세히 언급하겠습니다. 1) 조절효과를 보는 논문  연구모형 그림은 아래와 같습니다.   통상 이 경우에 Baron & Kenny의 위계적 회귀분석을 해야 한다고 하는데 그냥 회귀분석에 불과합니다.  연구모형..

사회과학논문에서 가장 많이 사용되는 연구방법론은 조절효과를 보는 Baron & Kenny(1986) 회귀분석이고요, 또 하나는 매개변수가 들어 있는 구조방정식 모형입니다. 이건 대부분 AMOS를 이용하여 분석하는데 최근에는 Baron & Kenny 방식에서 발전된 프로세스 매크로도 가끔 사용합니다.  그럼 이것 말고 다른 통계 방법론이 없을까 하는 생각이 들 수 있습니다. 위 방법론 등은 너무 흔해서요. 몇 가지 소개해 드리겠습니다.  1. 교차분석(Crosstabs Analysis) 이건 빈도분석에서 발전한 분석인데 옛날 석사 수준에서 자주 사용한 방법입니다. Likert 척도가 아닌 범주형 자료를 분석할 때 자주 사용하고 주로 현황을 파악하기 위해서 사용합니다.  예를 들어 한국을 방문한 외국인 관광..

이번에 쓸 이야기는 시차 t를 연속형 변수처럼 처리하는 경우입니다. 연속형 변수로 쓸 것이니까 시차를 ‘1차’, ‘2차’ 이렇게 문자열로 코딩하면 안되고 숫자 1, 2, 3 이렇게 코딩해야 합니다. 인터넷에 검색하면 혼합모형 쓰는 경우로 이 시차 t를 연속형으로 처리하는 예제가 많이 나옵니다. 만약 확률효과를 넣지 않으면, 즉 고정효과만 사용하면 이 모형은 독립변수가 시차 t인 단순회귀분석에 불과합니다. 물론 시간에 따라서 종속변수가 올라갔다 내려갔다 이렇게 변할 수 있습니다. 그럼 데이터에 t제곱, t3제곱 이런 변수를 만들어 회귀분석하면 됩니다. 그러나 시차 t가 상당히 커야 합니다. 단순히 시차 t 하나의 변수만 독립변수로 하는 경우랑, t, t제곱, t3제곱 이렇게 3개의 변수를 독립변수로 넣어 ..