이번에 쓸 이야기는 시차 t를 연속형 변수처럼 처리하는 경우입니다. 연속형 변수로 쓸 것이니까 시차를 ‘1차’, ‘2차’ 이렇게 문자열로 코딩하면 안되고 숫자 1, 2, 3 이렇게 코딩해야 합니다.
인터넷에 검색하면 혼합모형 쓰는 경우로 이 시차 t를 연속형으로 처리하는 예제가 많이 나옵니다.
만약 확률효과를 넣지 않으면, 즉 고정효과만 사용하면 이 모형은 독립변수가 시차 t인 단순회귀분석에 불과합니다. 물론 시간에 따라서 종속변수가 올라갔다 내려갔다 이렇게 변할 수 있습니다. 그럼 데이터에 t제곱, t3제곱 이런 변수를 만들어 회귀분석하면 됩니다. 그러나 시차 t가 상당히 커야 합니다.
단순히 시차 t 하나의 변수만 독립변수로 하는 경우랑, t, t제곱, t3제곱 이렇게 3개의 변수를 독립변수로 넣어 다항식으로 회귀분석 하는 경우와 비교하면 다항식으로 하는 경우가 무조건 적합도가 좋아집니다. 즉 R제곱값이 커집니다. 그러나 우리가 얻은 결과가 robust하지 않습니다. 즉 다른 사람이 똑같은 조건에서 데이터를 얻어 회귀분석을 하면 우리가 얻은 결과와 전혀 다른 결과가 나올 가능성이 큽니다.
그래서 회귀분석에서 이런 적합도의 문제를 해결하기 위해서 나온 다른 적합도의 기준이 수정결정계수(adjusted R제곱)입니다.
하여간 이 경우 개인간에 상수항과 기울기가 다르다고 가정하고 모형을 만들면 이젠 혼합모형의 확률효과를 쓴 것이 됩니다. 즉,
고정효과만 쓴 경우: Y=b0+b1*시차t+e
고정효과와 확률효과 다 쓴 경우: Y=(b00+b01)+(b10+b11)*시차t+e
이렇게 됩니다. 여기서 b01==> 정규분포(0, s1), b11==> 정규분포(0, s2)가 됩니다. 이건 개인간에 y절편과 기울기에서 변동이 있다는 이야기입니다.
이건 잘 보면 베이지안 느낌이 많이 듭니다. 즉 상수항 b0==> 정규분포(b01, s1), 기울기 b1==> 정규분포(b10, s2)라는 prior를 주는 것과 비슷한 것 같습니다.
베이지안 접근법과 혼합모형 접근법에 대해서 비교하는 것도 좋은 논문주제가 될 수 있겠습니다. 물론 일반 사회과학 논문이 아니라 통계학과 논문이죠. 아마 이미 누가 한 사람이 있을 겁니다.
햐여간 실제로 해보면 첫 번째 고정효과, 즉 시차 t를 독립변수로 하는 회귀분석을 하는 경우 지난번 글과 마찬가지로 고정을 클릭하고 시차 t를 선택하고, 통계량에서 모수 추정을 선택하면 회귀분석 결과표를 보여줍니다.
아래는 혼합모형을 한 경우와 회귀분석을 이용했을 때의 결과물입니다. 결과물이 서로 일치한다는 것을 알 수 있죠.

두 번째는 회귀분석에서 y절편과 기울기에서 개인간의 변동이 있다는 확률효과를 넣은 모형입니다. 즉, 모형은
고정효과와 확률효과 다 쓴 경우: Y=(b00+b01)+(b10+b11)*시차t+e
입니다. 이 경우 먼저 SPSS 혼합모형 처음 화면에서

시차를 독립변수로 사용할 것이니까 반복에 시차를 넣지 말고 공분산도 지정하지 마세요.
다음 공변량, 즉 연속변수에 시차를 지정하고

고정에서 차수를 지정하고 즉, 차수를 독립변수로 사용하겠다는 이야기입니다.

다음 변량을 선택한 다음 여기서도 시차를 선택합니다. 즉 시차 독립변수에 확률효과가 들어간다는 이야기입니다. 공분산 유형은 디폴트인 분산성분을 사용하고 마지막에 조합에 ID를 지정합니다. 그래야 확률효과가 나옵니다. 그리고 절편 포함도 체크를 해야 합니다. 그래야 y 절편에서도 확률효과가 들어간다는 것입니다.

마지막으로 앞으로 돌아가서 통계량에서 모수 추정과 공분산 모수 검증을 체크합니다.
그럼 다음의 결과를 얻습니다.
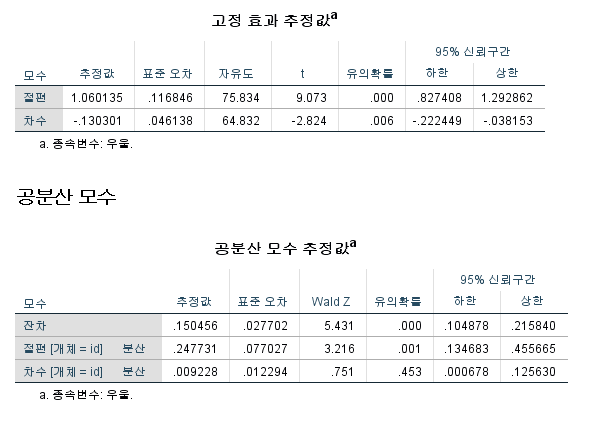
y 절편과 기울기가 처음 결과와 약간 다르다는 것을 알 수 있습니다.
그리고 y 절편에 있는 확률효과 분산 s1은 0이 아니다라고 판정이 났지만 기울기에서는 확률효과 분산 s2는 0이라는 판정이 났습니다.
그래서 기울기에서는 확률효과를 넣지 않고 고정효과만을 넣는 모형이 더 낫다고 볼 수 있습니다. 즉, 최종모형은 y절편에서만 확률효과를 넣고 기울기에서는 확률효과를 넣지 않는 모형이 바람직하다고 볼 수 있습니다.
최종모형: Y=(b00+b01)+b1*시차t+e
그런데 우리가 지금 해야 하는 분석에서는 실험 처지가 들어가 있는 집단이 있습니다. 이 집단에 따라서
Y=b0+b1*시차t+e
가 어떻게 달라지는가 하는 문제입니다.
단순하게 고정효과만 생각하면 앞에 쓴 글 Baron & Kenny의 조절효과 보기와 같습니다.
즉, 3개의 처지를 한 집단이 있다고 하죠. 집단A, 집단B, 집단c라고 하죠. 집단 A를 준거범주로 잡으면 위 회귀식은
집단A: Y=b0+b1*시차t+e
집단B: Y=(b0+집단B 효과)+(b1+집단B 효과)*시차+e
집단C: Y=(b0+집단C 효과)+(b1+집단C 효과)*시차+e
이렇게 되고
집단B에서 상수항에서 집단B 효과와 기울기에서 집단B 효과가 전부 0이라고 판정이 되면 준거 범주인 집단A와 집단B는 차이가 없다고 판단합니다. 즉 처치A와 처지B는 종속변수에서 전혀 차이가 없다고 판단합니다.
또 집단C에서 상수항에서 집단C 효과와 기울기에서 집단C 효과가 전부 0이라고 판정이 되면 준거 범주인 집단A와 집단C는 차이가 없다고 판단합니다. 즉 처치A와 처지C는 종속변수에서 전혀 차이가 없다고 판단합니다.
위 방법은 일반회귀분석에서 집단A=(0,0), 집단B=(1,0). 집단C=(0,1) 이렇게 코딩한 다음 시차t와 곱해서 상호작용항을 만들어 회귀분석을 하면 됩니다. 혼합모형에서는 고정에서 집단과 시차t를 선택해서 집단과 시차t와 집단*시차t을 선택하면 일일이 이진더미변수 만들고 곱하기 해서 상호작용항 만들고 하는 이런 복잡한 과정을 안 걸쳐도 결과물을 내어 줍니다.
단 집단B와 집단C에서 차이가 있는지는 판단할 수 없습니다. 이 경우 집단B=0, 집단C=1로 이진변수화를 한번 더 한 다음 다시 조절효과를 검증하는 수밖에 없는데 이게 문제가 좀 많습니다. 다중추론의 문제로서 좀 골치아픈 문제입니다.
여기서도 상수항과 기울기에서 개인의 편차를 고려한 확률효과를 넣을 수도 있습니다. 이런 것까지 요구할 것 같지는 않네요. 여러분이 직접 시도를 해 보세요.
'실험계획 > 혼합모형(mixed model)' 카테고리의 다른 글
| 혼합모형으로 실험효과보기2 (0) | 2023.09.28 |
|---|---|
| 혼합모형으로 실험효과 보기1 (0) | 2023.09.25 |
| 설문데이타로 혼합모형 확률효과로 분석하기 (0) | 2023.09.23 |
| 혼합모형을 이용하여 Baron & Kenny 조절효과 검증하기 (0) | 2023.09.18 |
| 혼합모형:이원분산분석하기 (0) | 2023.09.13 |