학위논문통계

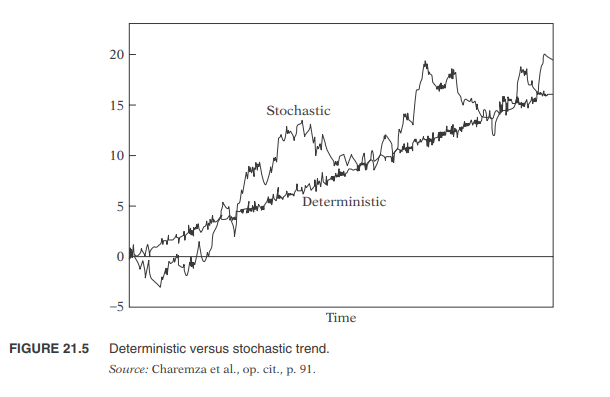
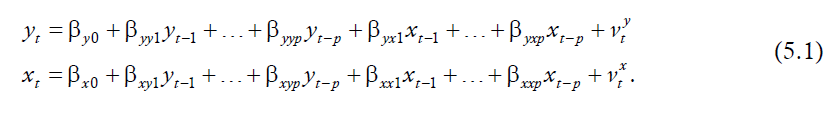1. R은 interpreter입니다.  아직 interpreter를 잘 모르는 분들이 있을 것 같은데요. 옛날부터 아니 지금까지 프로그램을 한다고 하면 프로그램 소스코드를 짠 다음 컴파일(compile)라는 것을 해야 합니다. 그래서 컴퓨터 안에서 돌아갈 수 있는 기계어 비슷한 것으로 바뀝니다. C, C++, 포트란, 맥의 Objective C 전부 다 compile 언어입니다. 다만 Java만 좀 다릅니다. 혼종이죠. R은 interpreter이고 compile 할 필요가 전혀 없습니다. 프로그램이 필요한 중요한 모듈은 이미 거의 다 만들어져 있고, 작업하는 사람은 이미 만들어진 모듈의 이름을 알아서 불러오기만 하면 됩니다.  최근에 인기가 많은 파이썬도 아마 interpreter 가능성이 높습니다...

1. var vecm 모형을 이해하기 위해서는 일단 VAR 모형을 단단하게나 이해를 해야 합니다. VAR 모형은  지금은 간단하게 관심있는 변수가 y, x 2개 밖에 없지만 3개의 경우 z 변수를 똑같은 형태의 수식으로 첨가하면 됩니다. 여기서 var 모형의 특징을 한번 간단히 보죠 t 시점은 y= (t 이전의 시점의 y들)+(t 이전의 시점의 x들)+t 시점의 혁신 v(y)t 시점은 x= (t 이전의 시점의 x들)+(t 이전의 시점의 x들)+t 시점의 혁신 v(x)  왼쪽의 연구변수 y(t), x(t)를 설명하는 오른쪽에는 혁신을 나타내는 동일 t 시점의 v(t)를 제외하고 모두 이전 시전 (t-1), (t-2)... 기의 변수들의 선형결합으로 되어 있습니다. 따라서 var 모형에서는 동일 t 시점의 ..

이왕 나온 김에 제 작업을 위해 미리 짜논 몇 개 함수를 소개하겠습니다. 모두 급하게 짠다고 해서 그리 잘 짠 프로그램은 아닙니다.   1. ave  구조방정식의 확인적 요인분석에서 AVE 값과 CR 값을 요구하는 경우가 있습니다. 이 값은 AMOS에서 구해 주지 않습니다. 시중에서 구조방정식 책을 사서 거기 공식에 맞춰 계산을 해야 합니다. AMOS 최근 버전에서는 구해 주는지는 잘 모르겠습니다. 하여간   ave nrnc mat  for (j in 1:nc){  a b cr mat[j,1]  f g ave mat[j,2] } mat;} 여기서 data는 확인적 요인분석 결과에서 나온 회귀계수와 표준오차를 말합니다. 이 함수가 최종적으로 return 하는 값은 mat이라는 matrix 형태의 값, 즉 ..

1. 요새 R이 크게 유행한다고 해서 글을 하나 올렸는데 아무도 읽은 사람이 없는 것 같습니다. 저도 미국에서 대학원 다닐 때 R의 이전 버전인 S를 매우 좋아했는데 이게 일반적인 통계 프로그램인 SAS, SPSS. BMDP과 완전히 다른 성격의 프로그램입니다. 아마 자료수가 엄청나게 많은 데이터를 자유로이 변형시킬때는 도움이 많이 될 겁니다.   2. sort, order, rank 지난 글 마지막에서 sort와 order를 소개했는데 썼다가 지웠습니다. 이거 다시 정리해서 글을 써야 할 것 같습니다. 비슷한 명령어로 rank가 있고요, 더구나 굉장히 중요한 응용이 있습니다.  만약 몇 만이 되는 정부 데이터가 있다고 하죠. 여기에 소득수준 변수가 있고요. 아니면 학교의 학생 수학 성적이 있다고 생각해..

R 과 R studio가 설치되어 있다고 가정하고 글을 쓰겠습니다.  R 모습은 이렇죠. 여기에 GUI(윈도우) 환경을 덮어 놓은게 R studio이고요.  R의 유래는 AT&T에서 개발한 S language입니다. 옛날부터 연구소나 대학원 이상에서는 Unix를 써 왔죠. 그래서 이공계나 통계학과에서는 공짜로 이 S을 사용해왔습니다. 그러다가 AT&T 가 상업용으로 팔아 버리고 인수한 회사는 망하고 이런 우연 곡절을 겪게 됩니다.  그러다가 사람들이 모여서 공짜 프로그램인 R을 개발하게 되고요. S도 S-plus라는 이름으로 상업용으로 여전히 사용되고 있습니다.  S-plus 모습을 한번 볼까요.   S와 R을 공부하기 위한 고전적인 유명한 책이 있습니다.  S Programming Language  입..

이번에는 지난번에 소개한 일반선형모형을 이용하여 실험효과를 검증하는 공변량분석을 해 보겠습니다. 실험의 계획은 대강 이렇습니다.  제약회사에서 새 다이어트 약을 개발했습니다. 그래서 이 약이 실제로 체중감소에 도움이 되는지 검증을 하고자 합니다.  먼저 2개의 집단을 뽑습니다.  하나는 실험집단으로 실험기간동안 다이어트 약을 투입할 집단입니다. 하나는 통제집단으로 실험기간동안 아무것도 하지 않을 집단입니다.  왜 이렇게 복잡하게 2개의 집단을 만들어서 실험을 할까요. 만약 일반인이 생각하듯 어떤 집단에 다이어트 약을 처방한 뒤 처방 전과 처방 후에 몸무게를 재면 어떤 문제가 생길까요. 만약 우리가 체중 감소를 위해 다이어트 약을 먹기로 결심한다면 단순히 다이어트 약만 먹지를 않습니다. 어떤 사람은 운동도..

논문을 쓰기 시작한다든지 해서 통계를 잘 해야 하겠다고 처음부터 과욕을 부리기 시작하시는 분들이 종종 계십니다. 그런데 공부하다 보면 일반선형모형, 일반화선형모형 이런 이야기를 부딪치면 바로 좌절을 하시는 분들이 많습니다. 너무 걱정하지 마십시오. 여러분이 평생 통계분석 논문을 써도 일반선형모형이나 일반화선형모형을 자세히 부딪칠 일이 없습니다.  1. 먼저 일반화선형모형(Generalized Linear Model)입니다.  통상 회귀분석의 종속변수는 정규분포를 가정합니다. 일반화선형모형은 종속변수가 정규분포가 아닌 경우를 다루는 모형입니다.  대표적으로 이항분포, 지수분포, 포아송분포 등 다양한 분포가 있을 수 있습니다. 그러나 여러분이 평생 이쪽 공부에서 실제로 부딪치는 경우는 이항분포의 경우 딱 한..

여기에 있는 내용은  Gujarati의 계량경제학 박완규, 홍성표 번역  이 책의 제일 뒤 부분에 있는 내용입니다. 자세한 내용은 이 책을 참조하시기 바랍니다.    지난 글에서 비정성 시계열의 대표적인 예로 random walk 프로세스를 소개했는데요. 이것만으로 충분하지 않죠. 이 random walk 프로세스는 평균은 계속 일정하거든요. 단지 분산이 시간이 흘러감에 따라 무한대를 향해 증가하는 변수이죠. random walk 프로세스는 우리에게 매우 익숙한 프로세스입니다. 브라운 운동이라고 아시죠. 공중에서 입자들이 움직이는 프로세스를 말하죠. 아인슈타인이 이 운동 법칙을 발견해서 노벨상을 받았죠.  임의행보 이외에도 많은 유형의 비정상 시계열 프로세스가 있습니다. 대표적인 것을 몇 개 소개하면  ..

1. 정상성 검증  시계열 분석을 할 때 제일 먼저 해야 할 것이 기초 기술통계를 구해 정규분포를 만드는 작업입니다. 통상 왜도나 첨도를 구하고 Log 치환을 합니다. 그 다음 해야 할 일이 연구 대상인 시계열 변수가 정상시계열인지 아니면 비정상시계열인지 판단하는 일입니다.  원 변수가 비정상 시계열이면 일차 차분해서 차분한 변수가 정상시계열로 변하는지 관찰하는 것입니다.  이때 가장 많이 쓰는 방법은 ACF, PACF plot을 그리고, 그리고 통계적으로 엄밀하게 하기 위해 ADF라는 검증방법을 쓰는 것입니다. 아래 그림을 참조하시기 바랍니다.    부동산시장수익률 D1.부동산시장수익률   표 47> 부동산시장수익률과 D1.부동산시장수익률 ADF 검증 시계열Z(t)1% 기각역5% 기각역10% 기각역근사..

지난번 공적분 글에서 다음과 같이 정리했습니다. 시계열 회귀모형  Y(t)=b0+b1*X(t)+e(t) 에서  X(t)와 Y(t)는 비정상 시계열이고 1) 오차항 e(t)가 정상 시계열이면 공적분 관계이고, 원 변수 X(t), Y(t)를 가지고 회귀분석을 할 수 있고  2) 오차항 e(t)가 비정상 시계열이면 Y(t), X(t), e(t)를 1차 차분하여 정상시계열로 변환한 다음 시계열 회귀분석을 실시한다.  이때 e(t)를 에러항이나 또는 시스템 외부에서 온 충격 이런 식으로 해석하는 것보다 두 개의 시계열 변수, 즉 Y(t)와 b0+b1*X(t)의 차이로 해석하는 것이 좋습니다. 지난번 공적분 글에서 든 예에서  하나의 Y(t)=부천의 20평 아파트 시세, X(t)=강남의 20평 아파트 시세라고 하면..