1. white noise 시계열
꼭 정규분포일 필요는 없지만
독립적이고 같은 분포를 갖는 시계열를 말합니다.
R 코드는
white<-rnorm(1000);
plot(1:1000, white, type="l", col=6);
2. random walk
주식시장을 보면 이동평균선이라는 그래프를 제공해주죠. 사실 이동평균선이 아니라 자기회귀가 이론적으로 더 맞는 말입니다.
AR(1) process를 보면
Y(t)=a*Y(t-1)+e(t)
이렇게 정의됩니다.
여기서 a=1이면 random walk이라고 한다. 이 경우 비정상시계열 모양을 합니다. a=1이면
Y(t)=Y(t-1)+e(t)
현재 시점 t에서 변수의 값 Y(t)는 하나 전 시점 (t-1)의 변수의 값 Y(t-1)과 같기 때문에 Y(t)는 정상시계열이라고 착각하기 쉽습니다. 그러나 뒤에 붙은 오차항 e(t) 때문에 이 경우는 비정상 시계열이 됩니다.
|a|<1 ==> 정상 시계열
|a| >=1 ==> 비정상 시계열이 됩니다.
이 AR(1) 모형은 정상시계열과 비정상시계열을 나누는 중요한 이론적 근거나 가설 검증의 이론이 되기 때문에 매우 중요합니다.
다음은 a의 다양한 값에 대해서 Y(t)의 plot을 한번 그려보기로 하죠.
다음은
R 코드입니다.
randomwalk<-function(coeff){
rw<-1:100
for(i in 2:100){
rw[i]<-coeff*rw[i-1]+rnorm(1);
}
rw;
plot(1:100, rw, type="l", col=6);
legend(1.0, 2.5, legend=c(coeff));
}
a=0.5

a=0.8
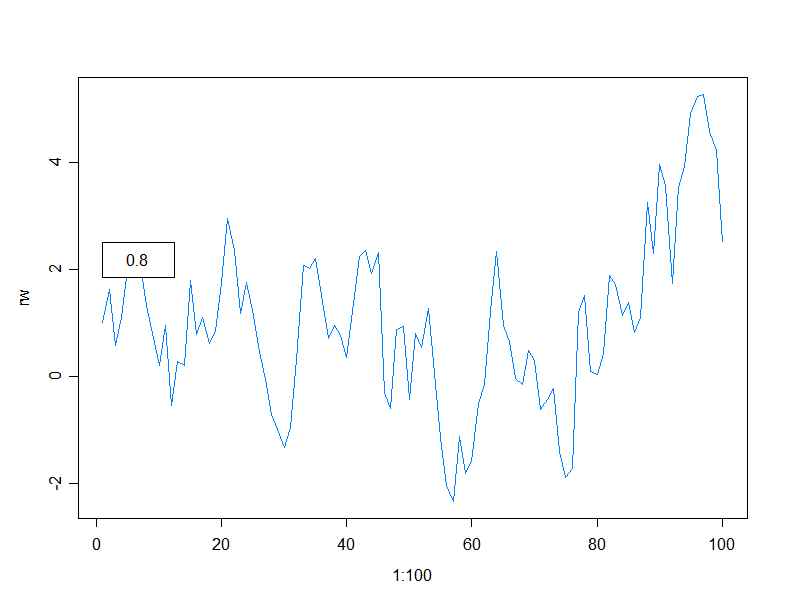
a=1
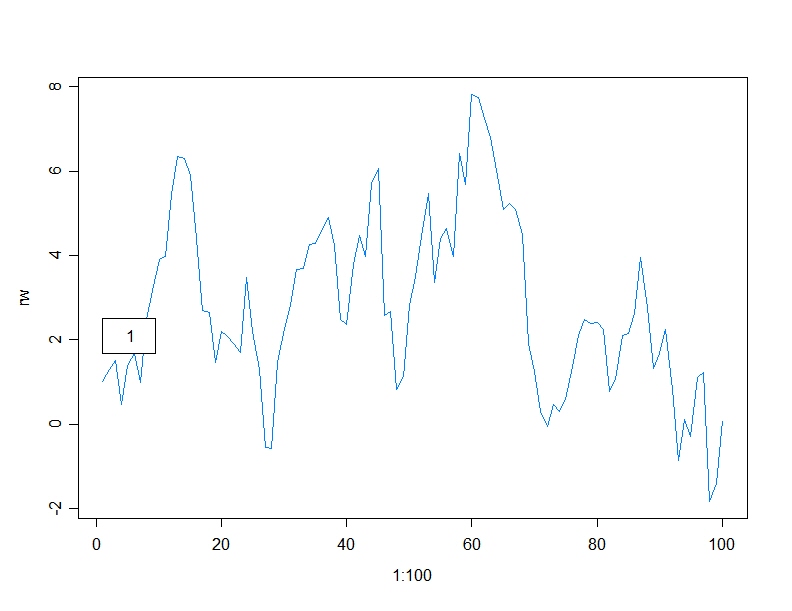
a가 1보다 조금이라도 크면 Y(t)의 모양이 확 바뀝니다.
a=1.02
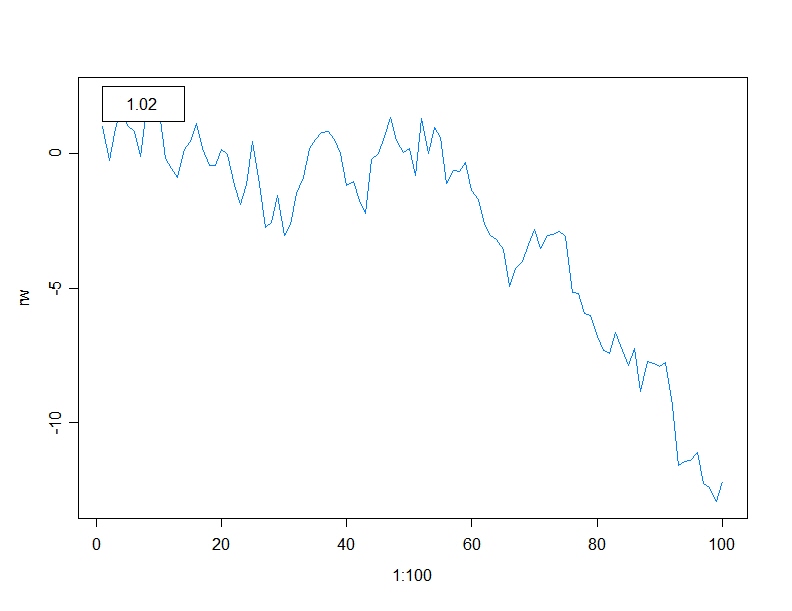
a=1.3
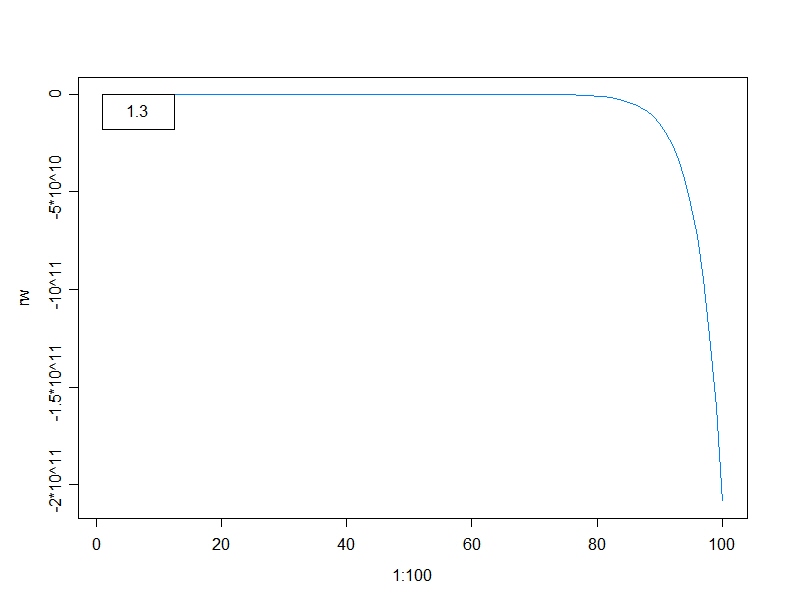
a=1.5

'계량경제 > 시계열회귀분석' 카테고리의 다른 글
| 정상성검증2: 비정상프로세스의 유형 (0) | 2024.06.20 |
|---|---|
| 정상시계열(안정적시계열)검증1: Random Walk (0) | 2024.06.18 |
| 공적분2 (0) | 2024.06.13 |
| 공적분관계1 (2) | 2024.06.05 |
| 시계열회귀분석과 패널회귀분석1 (1) | 2024.05.20 |