학위논문통계

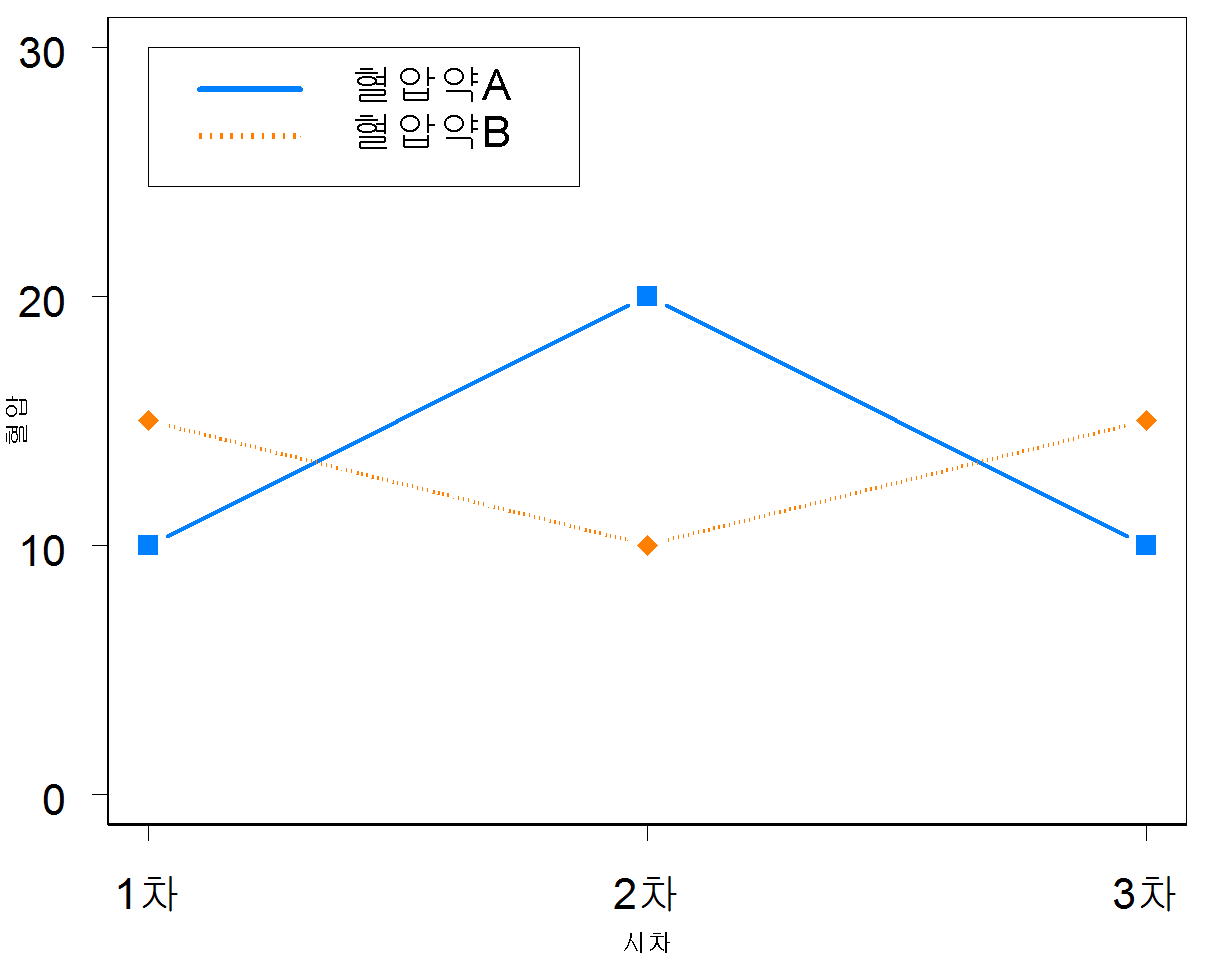
반복측정(repeated measure)은 왜 문제인가? 반복측정 이야기만 나오면 머리를 싸매시는 분들이 계시는데요.  반복측정은 실험의 효과를 보려는 경우, 그래서 의료나 보건쪽에서 자주 나오는 상황입니다. 특히 실험계획이라 해서 매우 복잡한 형태의 반복측정 모형이 여러 개 나옵니다.  실험의 효과를 측정하려면 동일한 개체에 대해서 여러번 측정을 해야 합니다. 동일한 개체에서 측정하기 때문에 각 측정치간에 서로 상관관계가 있다고 봐야 합니다.  학위논문에 가장 자주 쓰이는 방법인 사전 동질성, 사후 차이 검증도 사전에 한번 측정하고 사후에 또 한번 측정하고 2번 측정을 합니다. 효과의 지속성을 보려면 차후에 또 한번 볼 수 있죠.  그럼 반복측정할 경우 무슨 문제가 생길까요. 이걸 이해를 하려면 통계 ..

논문을 쓰기 시작한다든지 해서 통계를 잘 해야 하겠다고 처음부터 과욕을 부리기 시작하시는 분들이 종종 계십니다. 그런데 공부하다 보면 일반선형모형, 일반화선형모형 이런 이야기를 부딪치면 바로 좌절을 하시는 분들이 많습니다. 너무 걱정하지 마십시오. 여러분이 평생 통계분석 논문을 써도 일반선형모형이나 일반화선형모형을 자세히 부딪칠 일이 없습니다.  1. 먼저 일반화선형모형(Generalized Linear Model)입니다.  통상 회귀분석의 종속변수는 정규분포를 가정합니다. 일반화선형모형은 종속변수가 정규분포가 아닌 경우를 다루는 모형입니다.  대표적으로 이항분포, 지수분포, 포아송분포 등 다양한 분포가 있을 수 있습니다. 그러나 여러분이 평생 이쪽 공부에서 실제로 부딪치는 경우는 이항분포의 경우 딱 한..

이번에 쓸 이야기는 시차 t를 연속형 변수처럼 처리하는 경우입니다. 연속형 변수로 쓸 것이니까 시차를 ‘1차’, ‘2차’ 이렇게 문자열로 코딩하면 안되고 숫자 1, 2, 3 이렇게 코딩해야 합니다. 인터넷에 검색하면 혼합모형 쓰는 경우로 이 시차 t를 연속형으로 처리하는 예제가 많이 나옵니다. 만약 확률효과를 넣지 않으면, 즉 고정효과만 사용하면 이 모형은 독립변수가 시차 t인 단순회귀분석에 불과합니다. 물론 시간에 따라서 종속변수가 올라갔다 내려갔다 이렇게 변할 수 있습니다. 그럼 데이터에 t제곱, t3제곱 이런 변수를 만들어 회귀분석하면 됩니다. 그러나 시차 t가 상당히 커야 합니다. 단순히 시차 t 하나의 변수만 독립변수로 하는 경우랑, t, t제곱, t3제곱 이렇게 3개의 변수를 독립변수로 넣어 ..

혼합모형으로 실험효과를 볼 때 데이터 형태는 long format으로 해야 합니다. 패널데이타와 같은 모양입니다. 개체(subject) 집단 시차(time) Y X1 X2 A1 A 1 A1 A 2 A1 A 3 A2 A 1 A2 A 2 A2 A 3 A3 A 1 A3 A 2 A3 A 3 B1 B 1 B1 B 2 B! B 3 B2 B 1 B2 B 2 실험효과 데이터의 경우 개체는 주로 사람이나 동식물 등이 되지만 경영이나 경제 데이터에 많이 나오는 패널데이터의 경우 개체는 기업, 산업, 지역, 국가 등이 됩니다. 위 데이터에서 개체나 집단은 숫자 1, 2, 3 이렇게 표시해도 됩니다. 지난번 글에서 이야기했지만 실험의 상황이 매우 다양하기 때문에 결과물의 해석을 주의해서 해야 합니다. 즉 분산분석표의 유의적이..

지금까지 혼합모형에 대한 글은 혼합모형이라는 것을 이해하기 위해서 쓴 글이고 현실적으로 논문 분석에 적용할 수 있는 것은 아닙니다. 혼합모형이 논문 분석에 사용될 수 있는 분야는 실험효과 분석하는 부분입니다. 인터넷에 돌아다니는 혼합모형에 관한 글은 예로서 병원, 학교, 또는 학급 같은 예로 많이들 설명하는데 이때 표본추출 방식은 군집표본으로 일반적인 논문 분석에는 맞지 않는 표본추출 방식입니다. 이런 표본추출은 많은 돈이 들어가는 정부나 기업들이 사용하는 있는 표본추출 방법입니다. 1) 흔히 실험의 효과를 볼 때 많이 사용하는 방법은 실험집단과 통제집단을 만들어 사전, 사후 값을 측정하는 것입니다. 집단 사전 Y1 사후 Y2 실험집단 통제집단 2) 위 방법이랑 비슷한 것 같지만 완전히 다른 실험이 있습..

오늘은 설문지 데이터를 가지고 확률효과를 넣은 혼합모형을 쓸 수 없을까 하는 문제를 다뤄 보겠습니다. 모형은 편의상 가장 단순한 단순회귀분석으로 하죠. 독립변수가 여러개 들어가는 다중회귀분석도 마찬가지입니다. 독립변수는 변혁적 리더십, 종속변수는 자기효능감입니다. 즉 상사의 변혁적 리더십이 조직원의 자기효능감에 영향을 미치는가 하는 문제입니다. 그럼 모형식은 다음과 같습니다. 자기효능감=b0+b1*변혁적 리더십+오차 이걸 SPSS에서 회귀분석 메뉴에 가서 분석해도 되고 지난번 글에서 이야기했지만 혼합모형 메뉴에 가서 고정효과만 사용해서 분석해도 됩니다. 그럼 여기에 어떻게 하면 확률효과를 더 참가할 수 있을까 하는 문제입니다. 다음과 같이 하면 됩니다. 자기효능감=(b00+b01)+(b10+b11)*변혁..

이번에는 석사논문이나 저널논문에 자주 나오는 Baron & Kenny(1986)의 조절효과 검증을 혼합모형에서 어떻게 하는지 보겠습니다. 지난번에도 이야기했지만 여기서는 확률효과는 없고 오직 고정효과만 있습니다. 먼저 혼합모형 메뉴에 들어가면 첫 번째 메뉴가 뜹니다. 여기는 그냥 넘어갑니다. 이 메뉴는 패널데이터나 또는 반복측정, 또는 군집추출을 해서 아파트 단지, 병원, 또는 학교나 학급을 랜덤으로 선택할 경우만 이 메뉴를 사용합니다. 연구모형은 다음과 같습니다. 자기효능감=b0+b1*카리스마리더십+b2*연령+b3*(카리스마*연령) 여기서 성별같은 이진더미변수이면 별 문제가 없는데 연령같이 다범주, 즉 1=20대, 2=30대, 3=40-50대, 4=60대 이상 이렇게 코딩되어 있는 경우 조절효과를 보려..

지난번 글에서 고정효과와 확률효과에 대해서 설명을 했고요. 또 혼합모형은 기존의 통계 방법론의 확장된 분석 방법이라고 이야기했습니다. 즉 기존의 분산분석, 회귀분석, 조절효과 분석도 혼합모형을 이용해서 할 수 있습니다. 그래서 오늘은 좀 구체적으로 기존의 통계 방법을 혼합 모형에서 어떻게 할 수 있는지 구체적으로 설명하겠습니다. 그래서 혼합모형 이야기만 나오면 쫄아버리는 현상을 줄여볼까 합니다. 데이터는 흔히 여러분이 하는 설문조사 데이터입니다. 즉 횡단면 데이터입니다. 분석목적은 성별과 연령에 따라 자기효능감이 달라지는가이고 이원분산분석을 할 겁니다. 즉 자기효능감=성별+연령+성별*연령 입니다. 먼저 SPSS에서 혼합모형을 클릭합니다. 그럼 다음과 같은 메뉴가 뜹니다. 이 부분은 그낭 넘어갑니다. 즉 ..

혼합모형을 이해하기 상당히 힘든데요. 제가 공부할 당시 통계 교과서에서 나오지 않아서 체계적으로, 또는 학술적 권위가 있는 내용으로 배우지를 못했습니다. 그래서 여기서 쓴 내용은 제가 100% 옳다고 장담은 못하겠습니다. 저도 인터넷에서 자료 찾아보고(학술적 권위면에서 조금 약하죠), 저 나름대로 이리저리 시도해 보고 쓰는 내용입니다. 혼합모형이 왜 어려운가? 먼저 첫째, 이론적으로 이해를 해야 합니다. 둘째, 혼합모형은 기존의 대부분 모형, 즉, 분산분석, 회귀분석 등 또는 SPSS에 있는 repeated measure, variance component 등을 포함하는 매우 포괄적인 모형입니다. 그럼 이런 의문이 생길 수 있습니다. 기존에 내가 했던 방법은 틀린 것인가? 그럼 도대체 언제 이 혼합모형을..

이번은 이원분산을 이용해서 사전-사후, 실험-통제집단의 실험효과를 검증하는 방법을 설명하겠습니다. 이 경우는 데이터는 공변량 분석과 다르게 하나의 변수로 처리해야 합니다. 즉, 공변량 분석에서는 집단 사전측정값 사후측정값 0 3.5 3.7 0 3.25 3.19 1 2.85 3.25 1 3.41 3.54 0은 통제집단, 1은 실험집단이고요. 그러나 이원분산분석에서는 시차 변수를 추가하고 측정변수는 하나로 만들어야 합니다. 집단 시차 측정값 0 0 3.7 0 0 3.19 0 1 3.7 0 1 3.19 1 0 2.85 1 0 3.41 1 1 3.25 1 1 3.54 이원분산분석 식을 쓰면 Y=u+a+b+a*b+e 이렇게 됩니다. 원래 a와 b는 그리스 문자로 쓰는 것이 관례인데 여기 네이버 블로그에서는 수식편..