여기에 있는 내용은
Gujarati의 계량경제학
박완규, 홍성표 번역
이 책의 제일 뒤 부분에 있는 내용입니다. 자세한 내용은 이 책을 참조하시기 바랍니다.
지난 글에서 비정성 시계열의 대표적인 예로 random walk 프로세스를 소개했는데요. 이것만으로 충분하지 않죠.
이 random walk 프로세스는 평균은 계속 일정하거든요. 단지 분산이 시간이 흘러감에 따라 무한대를 향해 증가하는 변수이죠.
random walk 프로세스는 우리에게 매우 익숙한 프로세스입니다. 브라운 운동이라고 아시죠. 공중에서 입자들이 움직이는 프로세스를 말하죠. 아인슈타인이 이 운동 법칙을 발견해서 노벨상을 받았죠.
임의행보 이외에도 많은 유형의 비정상 시계열 프로세스가 있습니다.
대표적인 것을 몇 개 소개하면
1) Y(t)=b0+b1*t+e(t)
이건 그냥 단순한 독립변수 시간 t에 대한 회귀모형식이라 보시면 됩니다. TSP(trend stationary process)라고 합니다.
이 경우 안정적 시계열을 만들려면 먼저 회귀분석을 해서 bo와 b1을 추정한 다음 오차 e(t)가 아닌 잔차(residual)를 구하면 됩니다.
r(t)=Y(t)-(추정b0+추정b1*t)
이 과정을 추세제거(detrending)라고 합니다.
2) Y(t)=b0+Y(t-1)+e(t)
이 프로세스를 drift가 있는 random walk 모형이라 합니다. 앞에 상수항, y 절편인 bo가 있죠.
지난번 random walk 모형 조사할 때와 같은 기법으로 풀어 헤치면
Y(t)=b0+b0+Y(t-2)+e(t-1)+e(t)
= b0+b0+b0+Y(t-3)+e(t-2)+e(t-1)+e(t)
=Y(0)+t*b0+∑e(t)
drift가 없는 random walk 모형 Y(0)+∑e(t)과 비교하면
t*b0 항이 더 추가가 된 것이죠. 시간이 흘러감에 따라 평균도 일차방정식 모양으로 증가하면서 분산도 random walk 프로세스처럼 커져가는 프로세스입니다.
이 프로세스도 1차 차분하면
Y(t)-Y(t-1)=b0+e(t)
이라서 정상시계열이 됩니다.
위의 1)을 확정적 추세라고 하고 2)를 확률적 추세라고 합니다.
그림으로 한번 보죠.
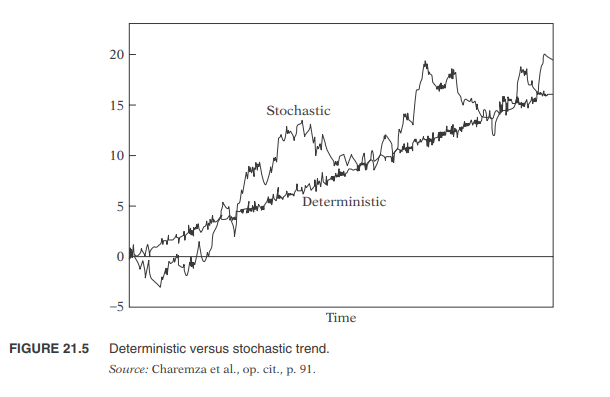
1)과 2)번 프로세스가 어떻게 다른지 감이 팍 오시죠.
3) Y(t)=b0+b1*t+Y(t-1)+e(t)
가장 복잡한 비정상 프로세스라 보면 되는데 표류(drift, 확률적 추세)와 확정적 추세가 결합된 형태입니다.
이 프로세스를 차분하면
Y(t)-Y(t-1)=b0+b1*t+e(t)
가 되어 정상시계열이 되지 못합니다.
위에서 여러 가지 유형의 비정상 시계열을 소개했는데 그럼 문제가 뭔가 하는 점이죠.
정상시계열인지 비정상시계열인지 통계적 검증을 하려면
귀무가설 H0: 비정상 시계열이다.
대립가설 H1: 정상 시계열이다.
이렇게 되는데 random walk 모형에서
Y(t)=b1*Y(t-1)+e(t)
에서
귀무가설: b1=1
대립가설; b1<1
이렇게 변합니다.
그러나 위 가설 검증은 위에 소개한 비정상 시계열의 하나의 유형에 불과한 random walk 모형에만 적용이 되는 가설검증입니다.
위의 방법으로 가설검증한 것이 Dickey-Fuller 검증의 기본생각입니다.
다음에는 DF검증의 문제와 ADF검증을 간단히 설명하겠습니다.
'계량경제 > 시계열회귀분석' 카테고리의 다른 글
| vecm1 (0) | 2024.07.04 |
|---|---|
| 정상시계열(안정적시계열)검증1: Random Walk (0) | 2024.06.18 |
| 공적분2 (0) | 2024.06.13 |
| white noise, AR(1), Random walk (0) | 2024.06.09 |
| 공적분관계1 (2) | 2024.06.05 |