1. var
vecm 모형을 이해하기 위해서는 일단 VAR 모형을 단단하게나 이해를 해야 합니다. VAR 모형은
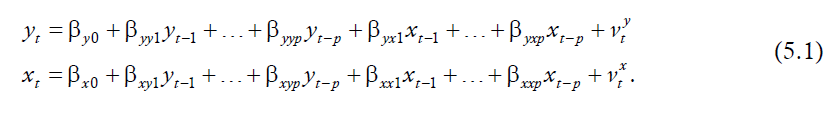
지금은 간단하게 관심있는 변수가 y, x 2개 밖에 없지만 3개의 경우 z 변수를 똑같은 형태의 수식으로 첨가하면 됩니다.
여기서 var 모형의 특징을 한번 간단히 보죠
t 시점은 y= (t 이전의 시점의 y들)+(t 이전의 시점의 x들)+t 시점의 혁신 v(y)
t 시점은 x= (t 이전의 시점의 x들)+(t 이전의 시점의 x들)+t 시점의 혁신 v(x)
왼쪽의 연구변수 y(t), x(t)를 설명하는 오른쪽에는 혁신을 나타내는 동일 t 시점의 v(t)를 제외하고 모두 이전 시전 (t-1), (t-2)... 기의 변수들의 선형결합으로 되어 있습니다.
따라서 var 모형에서는 동일 t 시점의 혁신 v(y)와 v(x)가 매우 중요한 요소로 작용할 거라 알 수 있습니다.
여기에 새로운 변수 z 가 추가되면 똑같은 형태의 수식만 추가되면 됩니다.
2. vecm
var 모형에 공적분 관계만 추가되면 vecm 모형이 바로 도출될 것 같지만 여전히 유사회귀 문제 때문에 회귀분석을 바로 할 수 없습니다.
그래서 일단 한번 차분을 해줘 왼쪽 연구변수들도 정상시계열로 만듭니다. 그런 다음 연립방정식 모양에 에러교정(error correction) 항목을 삽입합니다.

VECM 모형의 꽃은 요한슨(Johansen) 검증이라 할 수 있지만 사실 우리의 관심 대상은 아닙니다. 요한슨 검증은 VAR 모형에서 공적분 관계가 몇 개 있는가 단계별로 검증하는 것입니다. 요한슨 검증에서 common trend는 cointegrating relationship을 말합니다. 초기 이 이론 개발시 관용적으로 쓰인 용어입니다.
1단계 검증:
귀무가설: 공적분 관계가 하나도 없다
대립가설:최소한 1개 이상이 있다.
2단계 검증:
귀무가설: 공적분 관계가 최소한 하나는 있다.
대립가설: 최소한 2개 이상이 있다.
이렇게 계속 나가는 것입니다.
그러나 우리는 하나의 공적분관계가 있으면 됩니다. 그럼 y와 x와의 장기적 균형상태를 알 수 있고 이게 우리가 알고 싶어 하는 회귀분석의 결과가 됩니다.
'계량경제 > 시계열회귀분석' 카테고리의 다른 글
| 정상성검증2: 비정상프로세스의 유형 (0) | 2024.06.20 |
|---|---|
| 정상시계열(안정적시계열)검증1: Random Walk (0) | 2024.06.18 |
| 공적분2 (0) | 2024.06.13 |
| white noise, AR(1), Random walk (0) | 2024.06.09 |
| 공적분관계1 (2) | 2024.06.05 |